こんにちは、岩崎将史です。
今回は倍音について書きたいと思います。
前回に書いた【音楽制作の基礎】音とは？音の高さとは？音量とは？の続き的な意味合いがあります。
音楽に普段から接触する人には当たり前の知識です。
僕も大学の授業で、最初に伝える超基礎的なことです。
もし知らない人は、これを知っているだけで大きく音楽の捉え方が変わります。
作曲家、アレンジャーだけでなく、演奏家、サウンドエンジニアなど、音楽を仕事にする人は絶対に必要な基本の知識です。
振動の基本はサイン波
以前に書いた【音楽制作の基礎】音とは？音の高さとは？音量とは？では、音は物体の振動ということを説明しました。
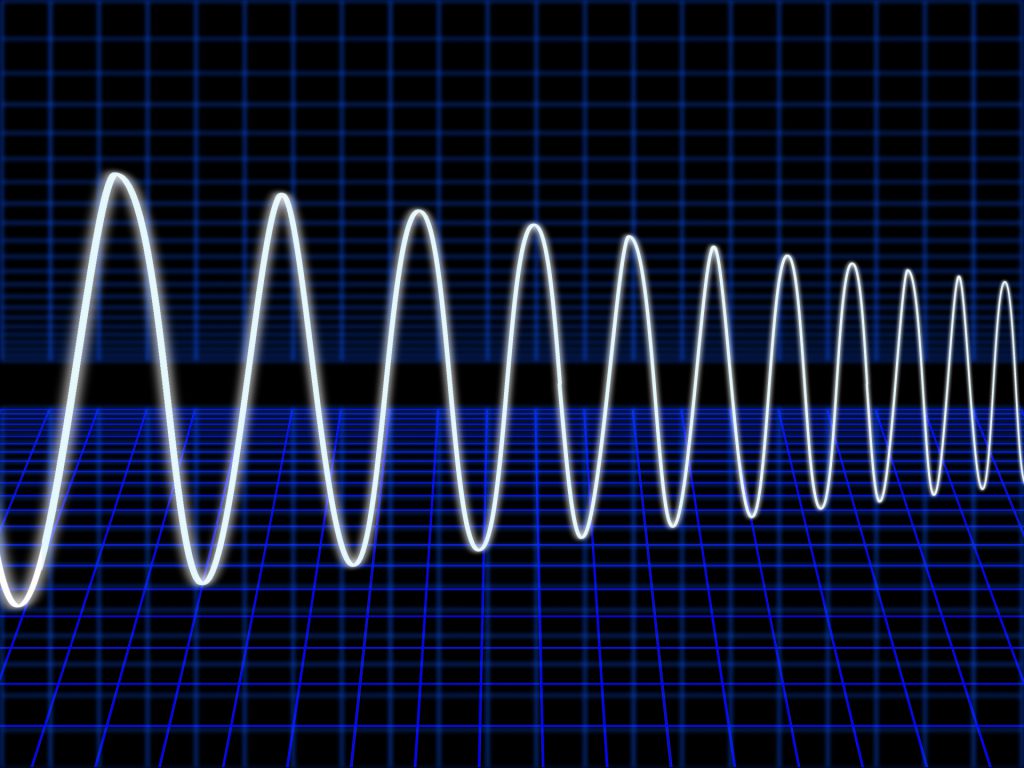
物体が振動するときの動きを図にするとサイン波と呼ばれる形になります。
上のCGの波の形がサイン波です。
サイン波の代表例は振り子です。
次の振り子の動画をみてください。
この振り子の動きを記録するとサイン波になります。
中学生の時に勉強していると思います。
あえて極論を書くと、この世界の音は全てサイン波の組み合わせできています。
いやいや、音の波形は他にも色々あるじゃん。
サイン波だけなく、矩形波、三角波、鋸波の3つを加えて４代波形というのがシンセサイザーや音響の基本で出てきます。
が、サイン波以外は極論をいうと現実世界では存続しえない音です。
もし「僕は本当の矩形波を聴いたことがある」という人がいたらやばいです。
理由を書くと今回のテーマからずれるので、別のブログ記事で書きたいと思います。
ちなみにサイン波の音はどんな音か？
440Hzのサイン波を聴いてみましょう。
聴く前に注意！
音量に気をつけてください。
最後にYouTube動画を貼っていますが、YouTubeのボリューム設定を最大にした時と同じ音量に合わせています。
スピーカーやイヤホンが大きくなっていると、びっくりするかもです。
ちょっとボリュームを絞って聴いみてから音量を調性してみてください。
これが440Hzのサイン波の音です。
音は物理的な運動エネルギーなので共振する
振り子の原理では共振というのを勉強したと思います。
音も同じ原理で共鳴します。
物の揺れ、振動なので同じ物理運動法則が働きます。
振り子の共振の動画です。
同じ長さの振り子が共振します。
たまたまじゃね〜の
というひねくれ者の方向けに、別の動画も貼っておきます。
これが共振になります。
同じ長さの振り子 ＝ 同じ音の高さ（ピッチ）の音
振り子は糸の長さで振幅、周期の時間が決まります。
- 短い→周期が速い
- 長い→周期が遅い
振り子の長さで周期が変わるのはこの動画で分かりやすく確認できます。
音 ≒ 振り子 ですので、
- 長い振り子 ≒ 低い音
- 短い振り子 ≒ 高い音
とイメージすると色々なことが分かりやすくなります。
同じ周期で揺れる振り子は共振します。
これが音として聴こえる振動エネルギーの場合は共鳴といいます。
正数倍音が共振する
先の動画では同じ長さの振り子が共振しました。
それ以外は揺れていません。
同じ長さだけが共振するのではなく、周期が整数倍であれば共振しやすいです。
1倍（同じ長さ）だけでなく、2倍、3倍、4倍と整数倍であれば共振しやすくなります。
嘘っぽい〜
というひねくれ者のために、分かりやすい動画を見つけたので貼っておきます。
NHKの昔の教育番組ですかね。
1倍の基本振動数に対して、2倍、3倍、4倍などの整数倍音が共振して鳴る
ということが動画から分かります。
昔、YouTubeでたくさんの振り子を吊るして、整数倍の振り子だけ揺れるという動画があったのですが今回は見つけられませんでした。
最後にピアノでの実験動画もアップしているので、それでも共振は確認できます。
整数倍の音を聴いてみよう
整数倍の周波数の音は共鳴するということは分かりました。
では整数倍の音とは、どんな高さの音なのか？
440Hzサイン波の周波数を変えて聴いていきます。
2倍の共振は1オクターブ
多くの音楽家が知っている周波数の代表は、
ラ＝A＝440Hz
です。
なぜ440Hz？
元々は435Hzを中心に色々あったけど1800~1900年代に掛けて測定器の登場と共に440Hzが推奨され、国際規格（ISO16）で決まりました。
まあ何でやっても自由だけどね。
音楽によって441Hzや442Hzとかもありますが、覚えるのにはキリの良い440Hzが語られます。ほとんどの電子楽器は初期設定が440Hzになっています。
440Hzとは1秒間に440回振動する周期の波ということです。
先ほどと同じですが、440Hz、ラ（A）のサイン波をもう一度聴いてみます。
ラ（A）の音を楽譜で表現すると、
となります。
では、2倍の880Hzのサイン波を聴いてみましょう。
ラ（A）です。
違うのはオクターブ上ということ。
楽譜で表すとこう。
音程（interval）は完全8度（octive）となります。
周波数が倍になると音の高さ（ピッチ）は1オクターブ上がるも〜
3倍の共振は１オクターブと完全５度
では次に3倍の音を出してみます。
440 x 3 = 1320
ですので1320Hzのサイン波を聴いてみましょう。
絶対音感や相対音感のある人ならミ（E）と分かります。
2倍の音との関係は完全５度になります。
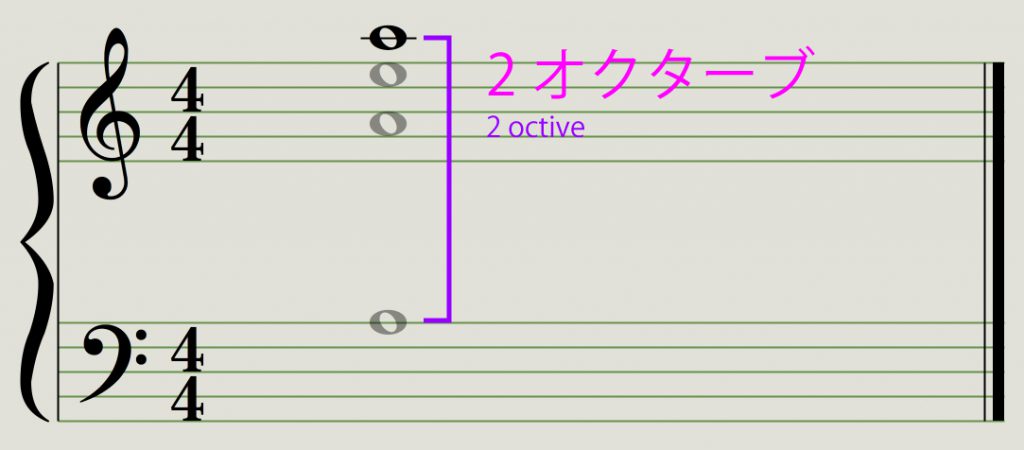
4倍の共振は2オクターブ上。
4倍の音を聴いてみましょう。
440 x 4 = 1760 ですので、1760Hzのサイン波です。
基音からすると2オクターブ上になります。
５倍の共振は2オクターブと長３度
440Hzの5倍は2.2kHzです。
聴いてみましょう。
ド# (=C#) になります。
楽譜に書くとこうなります。
1、2、３、４、５倍の音を鳴らすとメジャートライアドになる
ということで、知らなかった人もお気づきと思います。
1~5倍までの整数倍の音を並べると和音になります。
ラ・ド＃・ミ (A,C#,E) で長3和音 (major triad) になります。
Aメジャーと呼ばれるコードです。
1~5倍の周波数のサイン波を同時に聴いてみる
1~5倍の整数倍音を全て鳴らしてみます。
音だけだと分かりにくいので動画にしてみました。
ちゃんと「ラ・ド・ミ」のAメジャーコードになっています。
本物のピアノで倍音の共振を体感する
本物のピアノで実際の共振、共鳴が分かります。
動画にしてみました。
ノートPCのスピーカーだと良くわからないかもです。
ヘッドフォンかイヤホンだと良く分かると思います。
音楽理論は神様が作った物理法則
この倍音がコード、スケールといったあらゆる音楽理論の原理の元になっています。
というか理論が先ではなく倍音が聴こえるので、それに合わせてハーモニーが発展していきました。
つまりハーモニーとは神様が作ったこの世界の物理法則なんだも〜
です。
余談ですが昔、専門学校で作曲を教えていた時に、
僕の音楽は人が作った理論なんかに縛られたくないんです。
と一切講義を聞かず、作品は終始適当な音がなっている不協の連続というユニークな学生がいました。
説明しても「それすらも人間が勝手に考え出したことのはず」と頑なに受け入れてはくれませんでした。
まあ僕は、
生命の進化の過程では、異質な個は必要なことだも〜
と考えるタイプですので全く苦にはならなかったですが…。
今回はここまです。
この手の話は伝えたいことがたくさんさんあります。
が、音声や動画資料を用意するのが大変で、3日振りの更新になってしまいました。
早朝〜朝飯前の2~3時間くらいをいつもブログ書きの時間にしています。
少しづつでも暇を見つけて書いていきます。
では、また。
「音楽制作の基礎」の人気記事
なお共鳴という物理の基本原理は、程度の大小はあれ人間関係でも当てはまるかもしれませんね。人も物質ですし思考や行動は電気信号みたいですし。